TFC的铁砧问题

问题介绍

铁砧是TFC(群峦)模组中一个很重要的组成，是一种不可避免的合成物品的机制。当你打开一个铁砧时，会出现如下的界面。

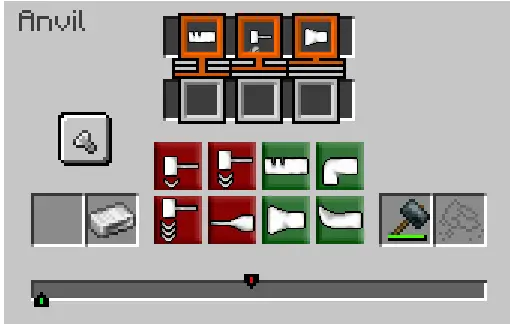
下面是一个进度条，你需要通过4个红色按钮和4个绿色按钮来将一个金属锭加工成你想要的东西。每一个按钮的会不同程度的将进度条左移或者右移，当进度条中的绿色游标正好对准红色目标时，你才会获取物品。只对算法感兴趣的童鞋请跳到 #算法模型。当操作次数足够小的时候会有更高的奖励。

问题调查

对于我来说，我非常讨厌这种重复性的工作，我希望我可以最省事的做完这样的操作。那么第一件事就是上github上翻番源码，虽然我找到过铁砧的计算器，但是我不是很满意这个算法的实现，那就只好自己调查一下了。首先很快找到TFC repo里跟铁砧有关的代码，很快就找到了这个 TerraFirmaCraft/src/main/java/net/dries007/tfc/common/recipes/AnvilRecipe.java。凭借着cpp基础随便就可以读Java代码不费一点劲。

    public int computeTarget(Inventory inventory)
    {
        return 40 + new XoroshiroRandomSource(inventory.getSeed())
            .forkPositional()
            .fromHashOf(id)
            .nextInt(154 - 2 * 40);
    }

    private boolean isWorkMatched(int work, int target)
    {
        final int leeway = TFCConfig.SERVER.anvilAcceptableWorkRange.get();
        return work >= target - leeway && work <= target + leeway;
    }

这是什么意思呢，work,就是那个绿条，你的当前进度，target,就是你的目标进度，我这一看有个leeway,单人里马上就给设置里，从此再也没有被这个问题烦恼过。 但是自从开始玩服务器之后，着就不够里。依照这个computeTarget，很明显每一个配方，竟然都是随机生成的。又翻了翻，翻到了TerraFirmaCraft/src/main/java/net/dries007/tfc/common/capabilities/forge/ForgeStep.java

public enum ForgeStep
{
    HIT_LIGHT(-3, 53, 50, 128, 224),
    HIT_MEDIUM(-6, 71, 50, 160, 224),
    HIT_HARD(-9, 53, 68, 192, 224),
    DRAW(-15, 71, 68, 224, 224),
    PUNCH(2, 89, 50, 0, 224),
    BEND(7, 107, 50, 32, 224),
    UPSET(13, 89, 68, 64, 224),
    SHRINK(16, 107, 68, 96, 224);
    ...
    ForgeStep(int step, int buttonX, int buttonY, int iconX, int iconY)
    {
        this.step = step;
        this.buttonX = buttonX;
        this.buttonY = buttonY;
        this.iconX = iconX;
        this.iconY = iconY;
    }
    ...

我基本上就算全都明白了

算法模型

有一序列的操作比如 [-15, -9, -6, -3, 2, 7, 13, 16]，你需要操作尽可能少的次数来让这些操作的值之和等于一个定值N。 0 < N < 150 对于有算法竞赛经验的同学来说，这个问题一看就会觉得太熟悉了，这不就是那个硬币问题么，妥妥的dp啊。就算是暴力都能解完吧。 不过对当时的我来说我还不知道什么是dp。 对我经历不感兴趣的请直接跳到#解法。

我的第一次尝试

写的其实不是非常工整，因为我需要的是最少的操作次数，那我就想，依照操作次数从低到高的顺序，列出所有的操作算出总和，如果找到了总和对了就停止。

let initial_list = [16, 13, 7, 2, -3, -6. - 9, -15]

let target_value = 100;

function reset() {
    return [
        initial_list.map(function (e) {
            return {
                value: e,
                path: [e]
            };
        })
    ];
}

let iterations = reset();

function iterate() {
    let last_iteration = iterations[iterations.length - 1];

    let iteration: {
        value: any;
        path: any[];
    }[] = [];

    initial_list.forEach(element => {
        last_iteration.forEach(it => {
            let value = it.value + element;
            let path = it.path.concat(element);

            if (value == target_value) {
                console.log(path);
                return path;
            }


            if (!last_iteration.find(e => e.value == value))
            ) {
                iteration.push({
                    value: value,
                    path: path
                });
            }
        });
    });

    iteration.sort(elem => Math.abs(elem.value - target_value))
    iterations.push(iteration)
}

我在写这段代码的时候感觉到其实有一个更优美更高效的解法，但是这个对我来说，好像差不多够用了。

解法

这道题看起来像是一个凑硬币的变体，带上具体路径的变体。但这个问题和dp不一样的地方是硬币的面值不能是负值，这就意味着硬币每加一个，那么总和一定会更多。但在这里面，总和可能会更少。也就可能会出现dp[99] > dp[100]的情况。
实际上是个简单的bfs,不过这个rust版本花了我不知道多长时间才写出来。 回看我的第一次尝试，我只是跳过了上次迭代会产生的值，而不是所有迭代visit过的值，只要稍微改改判断的条件就可以了

fn anvil_solve(possible_ops: &mut Vec<i32>, target_value: i32) -> Vec<i32> {
    possible_ops.sort();

    if possible_ops.contains(&target_value) {
        return vec![target_value; 1];
    }

    let n = (target_value + possible_ops.last().unwrap()) as usize;

    let mut visited = vec![false; n];

    visited[0] = true;

    let mut iteration = possible_ops
        .iter()
        .map(|e| (*e, vec![*e; 1]))
        .collect::<Vec<_>>();

    let mut path = vec![0; 0];

    for _ in 0..n {
        let visited_clone = visited.clone();
        // this got me so confused, why do I must write this

        let this = iteration.iter().flat_map(|it| {
            let ops = possible_ops.iter().filter(|op| {
                let pos = (it.0 + *op) as usize;
                pos < n && !visited_clone[pos]
            });

            for op in ops.clone() {
                if it.0 + *op == target_value {
                    let mut found = it.1.clone();
                    found.push(*op);
                    path = found;
                }
                visited[(it.0 + *op) as usize] = true;
            }

            ops.map(|op| {
                let mut path = it.1.clone();
                path.push(op.clone());
                (it.0 + op, path)
            })
            .collect::<Vec<_>>()
        });

        iteration = this.collect();
    }

    path
}

pub fn main() {
    let mut anvil_actions = vec![-15, -9, -6, -3, 2, 7, 13, 16];
    for step in anvil_solve(& mut anvil_actions, 25) {
        print!("{} ", step);
    }
    
}

用rust开发确实是十分坐牢就是了，写起来感觉像是面向2生命周期编程，代码行数多了10行但是时间花了不知道多多少

Table

1: 16 -15 
2: 2 
3: 16 2 -15 
4: 13 -9 
5: 13 7 -15 
6: 13 2 -9 
7: 7 
8: 16 7 -15 
9: 7 2 
10: 16 -6 
11: 13 13 -15 
12: 16 2 -6 
13: 13 
14: 7 7 
15: 13 2 
16: 16 
17: 16 16 -15 
18: 16 2 
19: 16 16 2 -15 
20: 13 7 
21: 7 7 7 
22: 13 7 2 
23: 16 7 
24: 16 16 7 -15 
25: 16 7 2 
26: 13 13 
27: 13 7 7 
28: 13 13 2 
29: 16 13 
30: 16 7 7 
31: 16 13 2 
32: 16 16 
33: 13 13 7 
34: 16 16 2 
35: 13 13 7 2 
36: 16 13 7 
37: 16 7 7 7 
38: 16 13 7 2 
39: 16 16 7 
40: 13 13 7 7 
41: 16 16 7 2 
42: 16 13 13 
43: 16 13 7 7 
44: 16 13 13 2 
45: 16 16 13 
46: 16 16 7 7 
47: 16 16 13 2 
48: 16 16 16 
49: 16 13 13 7 
50: 16 16 16 2 
51: 16 13 13 7 2 
52: 16 16 13 7 
53: 16 16 7 7 7 
54: 16 16 13 7 2 
55: 16 16 16 7 
56: 16 13 13 7 7 
57: 16 16 16 7 2 
58: 16 16 13 13 
59: 16 16 13 7 7 
60: 16 16 13 13 2 
61: 16 16 16 13 
62: 16 16 16 7 7 
63: 16 16 16 13 2 
64: 16 16 16 16 
65: 16 16 13 13 7 
66: 16 16 16 16 2 
67: 16 16 13 13 7 2 
68: 16 16 16 13 7 
69: 16 16 16 7 7 7 
70: 16 16 16 13 7 2 
71: 16 16 16 16 7 
72: 16 16 13 13 7 7 
73: 16 16 16 16 7 2 
74: 16 16 16 13 13 
75: 16 16 16 13 7 7 
76: 16 16 16 13 13 2 
77: 16 16 16 16 13 
78: 16 16 16 16 7 7 
79: 16 16 16 16 13 2 
80: 16 16 16 16 16 
81: 16 16 16 13 13 7 
82: 16 16 16 16 16 2 
83: 16 16 16 13 13 7 2 
84: 16 16 16 16 13 7 
85: 16 16 16 16 7 7 7 
86: 16 16 16 16 13 7 2 
87: 16 16 16 16 16 7 
88: 16 16 16 13 13 7 7 
89: 16 16 16 16 16 7 2 
90: 16 16 16 16 13 13 
91: 16 16 16 16 13 7 7 
92: 16 16 16 16 13 13 2 
93: 16 16 16 16 16 13 
94: 16 16 16 16 16 7 7 
95: 16 16 16 16 16 13 2 
96: 16 16 16 16 16 16 
97: 16 16 16 16 13 13 7 
98: 16 16 16 16 16 16 2 
99: 16 16 16 16 13 13 7 2 
100: 16 16 16 16 16 13 7 
101: 16 16 16 16 16 7 7 7 
102: 16 16 16 16 16 13 7 2 
103: 16 16 16 16 16 16 7 
104: 16 16 16 16 13 13 7 7 
105: 16 16 16 16 16 16 7 2 
106: 16 16 16 16 16 13 13 
107: 16 16 16 16 16 13 7 7 
108: 16 16 16 16 16 13 13 2 
109: 16 16 16 16 16 16 13 
110: 16 16 16 16 16 16 7 7 
111: 16 16 16 16 16 16 13 2 
112: 16 16 16 16 16 16 16 
113: 16 16 16 16 16 13 13 7 
114: 16 16 16 16 16 16 16 2 
115: 16 16 16 16 16 13 13 7 2 
116: 16 16 16 16 16 16 13 7 
117: 16 16 16 16 16 16 7 7 7 
118: 16 16 16 16 16 16 13 7 2 
119: 16 16 16 16 16 16 16 7 
120: 16 16 16 16 16 13 13 7 7 
121: 16 16 16 16 16 16 16 7 2 
122: 16 16 16 16 16 16 13 13 
123: 16 16 16 16 16 16 13 7 7 
124: 16 16 16 16 16 16 13 13 2 
125: 16 16 16 16 16 16 16 13 
126: 16 16 16 16 16 16 16 7 7 
127: 16 16 16 16 16 16 16 13 2 
128: 16 16 16 16 16 16 16 16 
129: 16 16 16 16 16 16 13 13 7 
130: 16 16 16 16 16 16 16 16 2 
131: 16 16 16 16 16 16 13 13 7 2 
132: 16 16 16 16 16 16 16 13 7 
133: 16 16 16 16 16 16 16 7 7 7 
134: 16 16 16 16 16 16 16 13 7 2 
135: 16 16 16 16 16 16 16 16 7 
136: 16 16 16 16 16 16 13 13 7 7 
137: 16 16 16 16 16 16 16 16 7 2 
138: 16 16 16 16 16 16 16 13 13 
139: 16 16 16 16 16 16 16 13 7 7 
140: 16 16 16 16 16 16 16 13 13 2 
141: 16 16 16 16 16 16 16 16 13 
142: 16 16 16 16 16 16 16 16 7 7 
143: 16 16 16 16 16 16 16 16 13 2 
144: 16 16 16 16 16 16 16 16 16 
145: 16 16 16 16 16 16 16 13 13 7 
146: 16 16 16 16 16 16 16 16 16 2 
147: 16 16 16 16 16 16 16 13 13 7 2 
148: 16 16 16 16 16 16 16 16 13 7 
149: 16 16 16 16 16 16 16 16 7 7 7 
150: 16 16 16 16 16 16 16 16 13 7 2 
151: 16 16 16 16 16 16 16 16 16 7 
152: 16 16 16 16 16 16 16 13 13 7 7 
153: 16 16 16 16 16 16 16 16 16 7 2 

后续

其实看的源码仔细一点就能发现原作者就写了个解，就在 TerraFirmaCraft/src/main/java/net/dries007/tfc/common/capabilities/forge/ForgeStep.java 里下面。

    static
    {
        PATHS = new int[LIMIT];
        Arrays.fill(PATHS, -1);
        PATHS[0] = 0;

        final IntPriorityQueue queue = new IntArrayFIFOQueue();
        final IntList buffer = new IntArrayList(8);

        int reached = 1;
        queue.enqueue(0);
        for (int steps = 1; reached < LIMIT; steps++)
        {
            while (!queue.isEmpty())
            {
                final int value = queue.dequeueInt();
                for (ForgeStep step : VALUES)
                {
                    final int nextValue = value + step.step;
                    if (nextValue >= 0 && nextValue < LIMIT && PATHS[nextValue] == -1)
                    {
                        PATHS[nextValue] = steps;
                        buffer.add(nextValue);
                        reached++;
                    }
                }
            }
            buffer.forEach(queue::enqueue);
            buffer.clear();
        }
    }